트레이닝 데이터를 사용해 머신 러닝 모델을 훈련하는 목표 중 하나는 모델이 본 적이 없는 데이터(혹은 레이블이 없는 데이터, 테스트 데이터)에서도 좋은 성능을 나타내게끔 일반화(generalize)를 하는 것이다.
즉, 훈련이 잘 된 모델은 학습하지 않은 데이터를 올바르게 분류하거나 결과를 예측할 수 있어야 한다.
예를 들어, MRI 결과를 가지고 암을 진단하는 네트워크를 훈련한다고 가정해보자. (관련 의료 정보에 대한 법은 무시하자.)
그 네트워크가 자신이 학습한 MRI 데이터로는 암을 잘 찾아내지만 학습하지 않은 환자의 MRI 데이터에는 제대로 암을 찾아내지 못한다고 하면 그저 쓸모없을 뿐만 아니라 자칫 생명을 잃을 수도 있는 모델이다.
위와 같은 현상이 오버피팅의 한 예인데, 오버피팅과 그에 반대되는 개념인 언더피팅이 무엇인지, 그리고 어떻게 오버피팅과 언더피팅을 막을 수 있는지 알아보자.
트레이닝 데이터와 테스트 데이터를 나누는 이유
이전에 MNIST 데이터를 다운받을 때 파라미터로 train=True 혹은 False을 줬던 기억이 있다.
한번쯤 데이터를 굳이 나누지 말고 모두 학습에 사용해서 모델을 빡세게 훈련시키면 더 좋지 않을까 생각할 수도 있다.
이제 트레이닝 데이터와 테스트 데이터로 분류하는 이유에 대해 알아보자.
머신 러닝 모델은 학습된 데이터를 바탕으로 처음 보는 데이터를 만났을 때에도 좋은 성능을 가져야 한다.
그렇기 때문에 모델의 성능을 평가하기 위해서는 이전에 본 적이 없는 데이터(테스트 데이터)로 성능을 테스트를 하는 것이 중요하다.
여기서 트레이닝 데이터와 테스트 데이터의 개념이 들어온다.
트레이닝 데이터는 모델을 훈련시키는데 사용된다.
여기에는 모델의 파라미터를 학습시켜 모델의 예측 값과 실제 결과 값 간의 오차를 최소화 하는 방향으로 훈련하는 것이 포함된다.
이렇게 훈련된 모델은 학습한 적이 없는 테스트 데이터로 성능이 평가되어서 얼마나 모델이 잘 일반화가 되었는지를 확인한다.
이제 몇 가지 경우로 모델에 대한 결과가 갈린다.
트레이닝 데이터와 테스트 데이터에서 모두 높은 성능을 나타내면 별 문제가 없을 것이다.
그런데 트레이닝 데이터에서는 높은 성능을 보이지만 테스트 데이터에서는 성능이 낮을 경우 이를 오버피팅이라고 한다.
반면 두 데이터 모두 낮은 성능을 보일 경우는 언더피팅이라고 한다.
(트레이닝 데이터에서 낮은 성능을 보이지만 테스트 데이터에서 높은 성능을 보이는 경우는 거의 없고 이런 현상을 굳이 분류하자면 훈련이 덜 된 상태인 언더피팅에 가깝다.)
이제 두 가지 상황을 자세히 알아보자.
Overfitting, Underfitting 개념
오버피팅과 언더피팅(혹은 Overtraining, Undertraining)은 머신 러닝에서 모델이 학습된 데이터에 얼마나 잘 맞는지를 설명하는 두 가지의 중요한 개념이다.
먼저 언더피팅(Underfitting)은 모델이 데이터의 기본적인 특징을 학습하지 못할 때 발생한다.
이 경우 트레이닝 데이터와 테스트 데이터 모두에서 성능이 저하된다.
언더피팅이 발생하는 이유는 모델이 너무 단순하여 데이터의 특징을 파악할 수 없을 때 생긴다.
마치 데이터가 이차함수의 분포를 띄는데 일차함수로 이를 근사하려는 경우 즉, 모델의 파라미터들이 데이터의 복잡도에 비해 부족할 경우 언더피팅이 발생한다.
또는 모델의 파라미터는 트레이닝 데이터의 복잡도만큼 충분히 복잡하지만 학습을 충분히 진행하지 못한 경우에도 언더피팅이 발생할 수 있다.
오버피팅(Overfitting)은 학습 데이터에 너무 가깝게 모델이 훈련되었을 때 발생한다.
데이터에 비해 모델의 파라미터가 너무 많거나 모델이 너무 오랫동안 훈련된 경우 발생한다.
위와 같은 요인들은 모델이 학습하는 데이터의 특징을 일반화 하는 것이 아니라 트레이닝 데이터를 거의 암기하다시피 훈련이 진행되었기 때문에 발생한다.
따라서 모델이 데이터의 중요한 패턴을 파악할 수 있을만큼만 복잡하고, 훈련 데이터를 암기하지는 않을 정도로 훈련을 적당히 마치는 것이 중요하다.
이러한 균형점을 찾기 위해 적절한 모델 아키텍처, 정규화 기법, 및 훈련 세부 전략 등을 세우는 것이 필요하다.
직접 코드를 만들어 눈으로 확인해보는 Overfitting, Underfitting
직접 언더피팅과 오버피팅의 상황을 재현해보자.
먼저 평균값이 다른 두 그룹의 2D 가우시안 분포를 가지는 데이터를 만들어보자.
두 그룹의 색을 각각 red, blue로 설정하였다.
import torch
import numpy as np
import matplotlib.pyplot as plt
npoints = 50
red = torch.stack((torch.randn(npoints), torch.randn(npoints)), axis=1)
blue = torch.stack((torch.randn(npoints)+1.5, torch.randn(npoints)+1.5), axis=1)
plt.figure(figsize=(5,5))
plt.scatter(red[:,0], red[:,1], c='r');plt.scatter(blue[:,0], blue[:,1], c='b')
plt.show()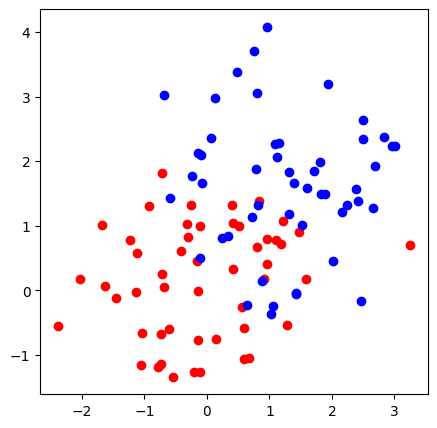
이제 위의 점을 분류할 것이다.
분류한 다음엔 x와 y가 -4 부터 4까지 모든 점들에 대해 모델이 점을 빨간색으로 구분하는지 파란색으로 구분하는지 알아볼 것이다.
(예를 들어, 위의 좌표평면에 (-2, 3)에는 점이 안 찍혀있지만, 이 점을 훈련한 모델에 넣었을 때 빨간색으로 구분할지 파란색으로 구분할지를 알아보겠다는 이야기다. 설명이 내가 봐도 좀 그렇지만 이후에 나올 훈련 결과를 보면 이해가 될 것이다.)
이제 모델을 만들고 각 데이터 포인트도 학습에 사용할 수 있도록 변형하자.
class Model(torch.nn.Module):
def __init__(self, n):
super(Model, self).__init__()
self.n = n
self.fc1 = torch.nn.Linear(2,n)
self.fc2 = torch.nn.Linear(n,n)
self.fc3 = torch.nn.Linear(n,1)
def forward(self, x):
#x = torch.stack([x**i for i in range(self.n+1)], axis=1)
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = torch.sigmoid(self.fc3(x))
return x
xs = torch.cat([red,blue])
ys = torch.cat([torch.ones(len(red)), torch.zeros(len(blue))])일단 모델의 입력은 점의 x, y좌표가 들어가야하므로 2개이고 출력은 빨간색인지(1) 파란색인지(0)를 출력해야하므로 1개이다.
중간의 히든 레이어를 두었고 이 히든 레이어의 노드 수를 n으로 둬서 직접 설정할 수 있게 하였다.
이제 모델을 트레이닝 하는 코드를 살펴보자.
def showmodel(n):
m = Model(n)
lossf = torch.nn.BCELoss()
optim = torch.optim.AdamW(m.parameters(),lr=0.01)
for _ in range(2500):
optim.zero_grad()
fs = m(xs)
loss = lossf(fs.view(-1), ys)
loss.backward()
optim.step()
x1,x2=np.meshgrid(np.linspace(-4,4), np.linspace(-4,4))
col = m(torch.tensor(np.dstack([x1,x2])).float())
plt.imshow(col.detach().numpy(),origin='lower',extent=(-4,4,-4,4), cmap='bwr')
plt.scatter(red[:,0], red[:,1], c='r',edgecolor='k');plt.scatter(blue[:,0], blue[:,1], c='b', edgecolor='k')
plt.show()모델을 2500번 훈련하고 x와 y가 각각 [-4, 4] 영역에서 모델이 점을 어떻게 분류하는지를 그림으로 출력해준다.
이제 n이 1, 2, 8, 32, 256일 때를 살펴보자.
n = 1
showmodel(1)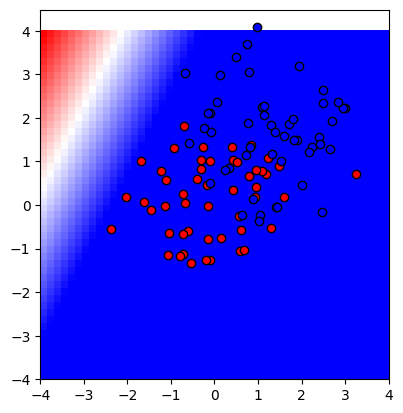
모델이 데이터를 잘 구분하고 있는가에 대한 판단은 여러분에게 맡기겠다.
다만 이 경우 모델의 성능이 트레이닝 데이터이든(점), 테스트 데이터이든(좌표 평면) 아주 별로인 것을 확인할 수 있다.
즉, 언더피팅이 되었다고 말할 수 있다.
n = 2
showmodel(2)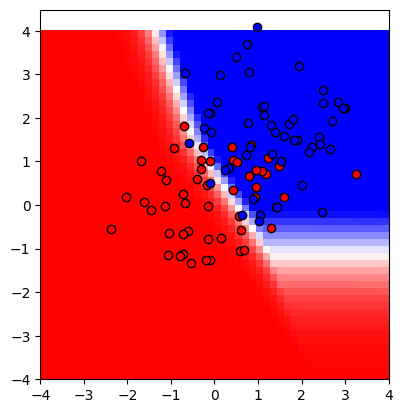
n = 8
showmodel(8)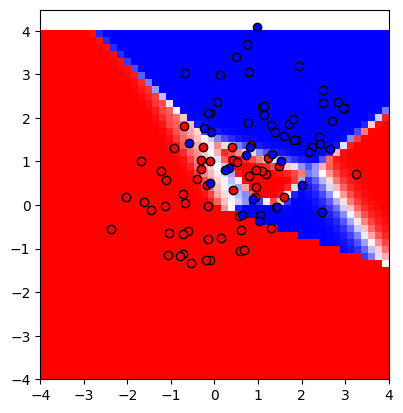
n = 32
showmodel(32)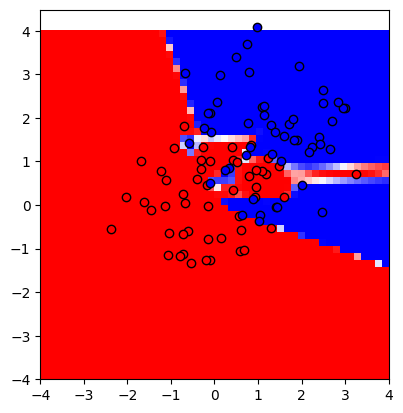
n = 256
showmodel(256)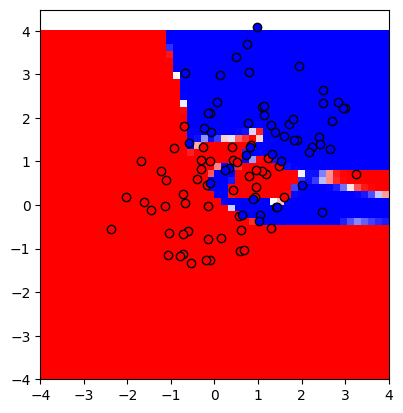
내 전공이 수학이나 컴퓨터가 아니기 때문에 어느 순간이 가장 낫다고는 단정지어 말하지 못하겠지만,
데이터를 평균값만 다른 가우시안 분포를 가지도록 설정했기 때문에 아마 중간에 적당한 직선을 그어 빨간점과 파란점을 분류하는게 데이터의 특징을 잘 일반화 했다고 말해볼 수 있다.
하지만 히든 레이어의 노드 수가 많아질수록 모델이 마치 학습했던 데이터를 암기하여 분류하는듯한 느낌을 위에서 확인할 수 있다.
즉, 모델의 파라미터가 데이터에 비해 너무 많기 때문에, 혹은 훈련을 너무 많이 했기 때문에(에포크가 너무 크기 때문에) 모델이 오버피팅이 되었다는 이야기다.
Bias-Variance Tradeoff
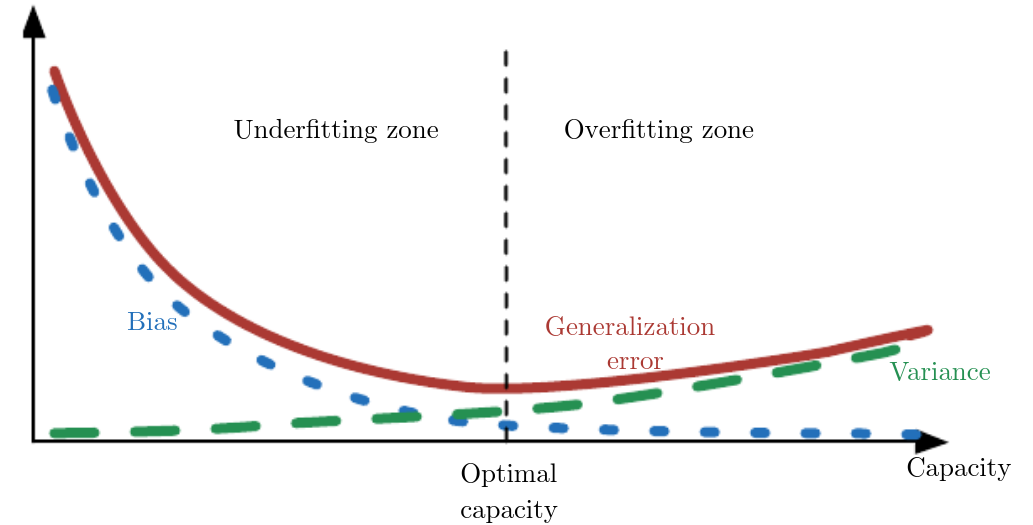
중요하다고 하면 중요하고 아니라고 하면 아닌 위의 그래프는 Bias-Variance tradeoff으로 불리는 그래프이다.
참고로 x축의 Capacity는 모델의 복잡성을 뜻한다.
이 그래프가 모델의 언더피팅과 오버피팅을 막아준다는 이야기는 아니다.
다만 모델의 단순함과 복잡함 사이에서 균형을 맞춰야 한다는 개념을 알려주고 어디가서 아는 척도 할 수 있게 해준다.
파란 점선인 Bias는 모델의 예측 값과 실제 값의 차이를 말한다.
즉, Bias가 큰 모델은 모델이 단순하거나 정확한 예측을 하기에 정보가 충분하지 않아서 발생한다.
반면 Variance는 서로 다른 입력이 주어졌을 때 모델의 예측이 얼마나 변화하는지를 뜻한다.
이 값이 높은 모델 즉, 복잡한 모델은 작은 입력의 변화, 이를테면 작은 노이즈에도 민감하게 반응해서 다른 답을 내놓는다.
(위의 가장 복잡한 모델인 n=256 일 때, 중앙 부근에서 값이 조금만 달라져도 파란 영역과 빨간 영역이 왔다갔다 하는 것을 볼 수 있다.)
결국 위의 그래프가 우리에게 해주는 말은 모델이 데이터의 여러 특징을 잘 추출할 수 있을 정도로 복잡해야하지만 너무 복잡해진 나머지 노이즈에 민감해지면 안된다는 것이다.
오버피팅 예방하기
오버피팅을 막는 보편적인 네 가지 방법을 살펴보자.
1. 데이터 키우기
데이터의 양이 적으면 모델이 데이터에서 노이즈와 같은 중요하지 않은 부분까지 학습할 우려가 생긴다.
따라서 데이터의 양을 늘려 모델이 데이터의 일반적인 특성을 학습할 수 있도록 해서 오버피팅을 예방할 수 있다.
데이터의 양이 적을 경우 Data Augmentation이라는 방법을 사용해 기존 데이터를 사용해 새로운 데이터를 만들어낼 수 있는데, 이미지의 경우 이미지를 회전시키거나 약간의 노이즈를 추가하는 등의 방법을 사용할 수 있다.
2. Early Stopping
Early stopping는 모델을 훈련하는 중 테스트 데이터 세트에서 모델의 성능을 모니터링하고 테스트 데이터 세트의 성능이 저하되기 시작하면(테스트 데이터 세트의 비용 함수의 값이 증가하기 시작하면) 훈련를 중지하는 작업을 말한다.
이렇게 하면 모델이 학습 데이터를 노이즈까지 계속 학습하는 것을 방지하고 모델이 새 데이터에도 잘 일반화되도록 할 수 있다.
3. 모델을 단순화 하기
모델이 필요이상으로 복잡할 경우 모델이 데이터의 불필요한 세부적인 부분까지 학습하게되기 때문에 모델을 단순화하므로 오버피팅을 예방할 수 있다.
4. Dropout
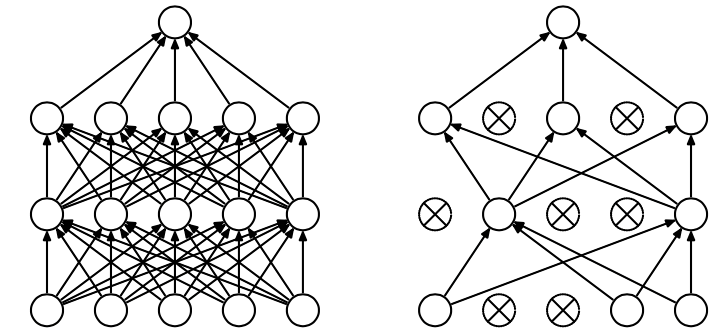
드랍아웃은 학습 시 신경망의 일부를 끊고 학습을 하는 것이다.
드랍아웃은 신경망이 특정 노드에 너무 많은 영향을 받는 것을 막아주고 매번 다른 조합의 노드를 사용하게 되어 좀더 일반적인 응답을 가지게 해준다.
5. Regularization
Regularization(정규화)을 사용하면 모델의 파라미터가 너무 커지는 것을 방지해서 모델이 훈련 데이터에 오버피팅 되지 않게 해준다.
주로 사용되는 정규화 방법으로 L1, L2, Elastic Net가 있는데 L1은 가중치의 절댓값에 제한을 걸고, L2는 가중치의 제곱에 제약을 준다. Elastic Net은 L1와 L2을 결합한 방식이다.
PyTorch에서는 L1, L2, Elastic Net 등의 Regularization을 적용하기 위해 weight_decay파라미터를 설정할 수 있다. 이 값이 클수록 Regularization 효과가 강해지며, 작을수록 Regularization 효과가 약해진다.
오버피팅과 언더피팅은 머신러닝에서 모델의 성능 저하로 이어질 수 있는 흔한 문제이다.
그러나 이러한 문제를 방지하기 위해 데이터를 증가시키거나 early stopping, 모델 복잡도 줄이기, dropout, 정규화 같은 오버피팅을 예방하기 위해 사용할 수 있는 몇 가지 기술이 있다.
이러한 방법을 적용하면 모델을 좀더 일반화 시켜서 보다 강력하고 정확한 모델을 만들 수 있다.
모델의 복잡성과 일반화 사이에서 올바른 균형을 찾는 것이 머신러닝에서 중요하다 점을 기억하자.
'머신 러닝 > Theory' 카테고리의 다른 글
| [Machine Learning] Hyperparameter Optimization on PyTorch (하이퍼파라미터 튜닝) 개념과 방법 (0) | 2023.03.22 |
|---|---|
| [Machine Learning] PyTorch로 Transfer Learning (전이 학습) 구현하기 (0) | 2023.03.08 |
| [Machine Learning] 옵티마이저(Optimizer) 이해 및 종류별 특징 (1) | 2023.03.03 |
