[Machine Learning] PyTorch로 로지스틱 회귀 구현하기 (Logistic Regression)

이번 글에서 알아볼 주제는 Logistic Regression이다.

먼저 예제를 통해 문제를 간단하게 알아보자.

---

Logistic function

먼저 logistic function을 알아보자.

로지스틱 함수는 다음 함수를 말한다.

Sigmoid function이라고도 부른다.

흔히 "turn-on" 커브라고도 하는데 데이터를 두 종류로 분류할 때 쓰인다.

데이터가 0인지 1인지, 개인지 고양이인지 구분할 때 사용한다.

Logistic Function

데이터가 어떤 모델에서 계산된 값이 있다고 하자.

그 값이 위의 그래프에서 y값이 0.5 이상이면 1(혹은 개), 0.5 이하이면 0(혹은 고양이)으로 분류할 수 있다.

즉, x축에서 0이상이면 분류를 1(혹은 개)로, 0이하이면 분류를 0(혹은 고양이)으로 하겠다는 이야기다.

 

이제 아래 데이터 분포를 생각해보자.

여기에 직선 하나만 그어서 빨간 점과 파란 점들을 어떻게 분류할 수 있을까

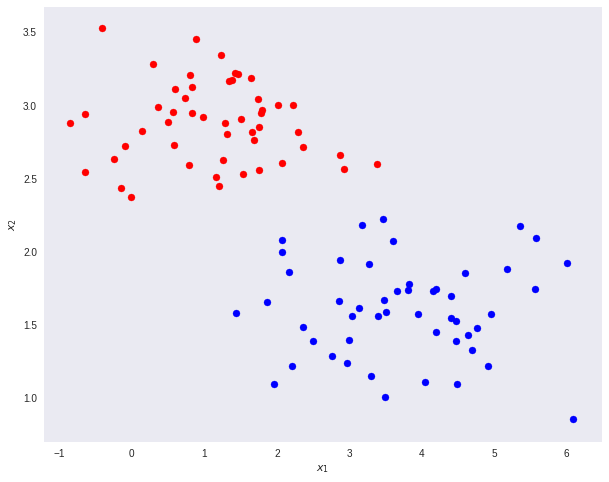
이제 아래 그림에 x축을 그어서 로지스틱 함수를 그릴 것이다.

어떻게 x축을 그어야 가장 높은 정확도(accuracy)를 갖도록 직선을 그을 수 있을까?

이런 식으로 긋는다는 이야기다.

먼저 아래 초록 선처럼 직선을 긋고 직선에 대해 점들을 정사영(projection)시켜보자.

그러면 아래 줄처럼 데이터들을 분류할 수 있고 이 점들을 로지스틱 함수의 입력이라고 생각해보자.

데이터를 직선에 정사영시키자

그러면 아래 처럼 로지스틱 함수를 그릴 수 있을 것이다.

로지스틱 함수를 씌우자

노란 영역에 데이터들이 많이 겹쳐있고 이 부분에서 정확도가 낮아질 것이다.

그러면 직선을 다시 그어서 정사영 시켜보자.

다시 그은 직선, 겹치는 부분이 없다.

보기가 불편해서 로지스틱 함수를 위에 덧씌우지는 않았지만 빨간 점들과 파란 점들이 잘 분류되었음을 이미 확인할 수 있다.

 

물론 위의 데이터는 설명을 위해 두 그룹 간에 약간의 유격을 두었다.

우리가 만나게 될 데이터는 저런 데이터보다는 아무리 잘 분류하더라도 약간의 겹치는 부분이 있을 수 있다.

이제 우리가 할 일은 최대한 겹치는 부분이 없도록 즉, 높은 정확도를 가지도록 직선을 긋는 일이고 이것을 Logistic Regression(로지스틱 회귀)라고 부른다.

---

Logistic Regression 구현하기

먼저 모델을 구현해보자.

저번 선형 회귀에서는 레이어가 하나였지만 이번에는 두 개를 사용해보자.

import torch
import torch.nn as nn

class LogisticRegression(nn.Module):
    def __init__(self):
        super(LogisticRegression, self).__init__()
        self.fc1 = nn.Linear(2, 8) # fc = fully-connected
        self.fc2 = nn.Linear(8, 1) # make sure the sizes are right
        
    def forward(self, x):
        # This is a typical pattern in torch code, reusing the
        # name x for succesive layers
        x = torch.sigmoid(self.fc1(x))
        x = torch.sigmoid(self.fc2(x))
        return x

 

데이터도 만들어보자.

import matplotlib.pyplot as plt
npoints = 100
red = torch.stack((torch.randn(npoints), torch.randn(npoints)), axis=1)
blue = torch.stack((torch.randn(npoints)+2, torch.randn(npoints)+2), axis=1)

plt.scatter(red[:,0], red[:,1], c='r')
plt.scatter(blue[:,0], blue[:,1], c='b')

데이터의 분포를 출력해보면 아래와 같다.

이제 이 데이터들을 최대한 분류해볼 것이다.

다만 모델에서 레이어를 두 번 사용했으므로 위에서 설명했던 것처럼 구분하는 선이 직선 하나는 아닌 점에 유의하자.

분류할 데이터

 

비용 함수와 옵티마이저와 타겟을 정해주자.

loss = torch.nn.BCELoss()
model = LogisticRegression()
optim = torch.optim.SGD(model.parameters(), lr=0.002)
zero = torch.full((100,1), 0.) # 0 for red
one = torch.full((100,1), 1.)  # 1 for blue

모델의 입출력에 맞게 데이터의 차원과 라벨을 설정해주자.

red_with_label  = torch.cat((red, zero), 1)
blue_with_label = torch.cat((blue, one), 1)

data = torch.cat((red_with_label, blue_with_label), 0)

모델을 훈련하는 코드를 짜보자.

훈련하는 방법은 선형 회귀와 비슷하다.

모델에 입력을 넣고 모델의 출력값을 타겟과 비교하여 비용함수를 계산한 다음, 모델의 파라미터를 그에 맞게 업데이트 하는 방법이다.

accuracy = []
epochs = 100

for epoch in range(1, epochs+1):
    for x in data:
        optim.zero_grad()
        pred = model(x[:2])
        Loss = loss(pred, x[2].view(1))
        Loss.backward()
        optim.step()
        
    red_acc = model(red) < 0.5
    blue_acc = model(blue) > 0.5
    acc = torch.cat((red_acc, blue_acc), 0)

    correct = 0
    for i in acc:
        if i == True:
            correct += 1

    accuracy.append(correct / len(data))
    
    print('Epoch {:3d}/{} Cost: {:.4f}'.format(
        epoch, epochs, accuracy[-1]
    ))

에포크에 따른 정확도는 accuracy에 저장되어있다.

아래 코드로 간단히 출력할 수 있다.

약 90%의 정확도를 가지고 있음을 확인할 수 있다.

plt.plot(accuracy)

epoch에 따른 accuracy

덧붙이자면 모델에 레이어를 더 추가하고 훈련을 더 많이 진행시키면 더 높은 정확도를 가지게 될 수 있다.

하지만 그런 모델의 경우 훈련한 데이터는 기가 막히게 잘 구분하지만 그만큼 학습된 데이터에 잘 맞도록 훈련되었기 때문에,

비슷한 분포의 데이터가 새롭게 추가되었을 때는 다시 성능이 낮아질 수 있다.

이를 오버피팅(과적합, overfitting)이라고 한다.

이름의 뉘앙스에서 느낄 수 있는 것처럼 별로 좋은 현상은 아니다.

오버피팅에 대한 이야기는 다음에 다뤄보도록 하자.

---

전체 코드는 아래와 같다.

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

npoints = 100

red = torch.stack((torch.randn(npoints), torch.randn(npoints)), axis=1)
blue = torch.stack((torch.randn(npoints)+2, torch.randn(npoints)+2), axis=1)

plt.scatter(red[:,0], red[:,1], c='r')
plt.scatter(blue[:,0], blue[:,1], c='b')

class LogisticRegression(nn.Module):
    def __init__(self):
        super(LogisticRegression, self).__init__()
        self.fc1 = nn.Linear(2, 8) # fc = fully-connected
        self.fc2 = nn.Linear(8, 1) # make sure the sizes are right
    def forward(self, x):
        # This is a typical pattern in torch code, reusing the
        # name x for succesive layers
        x = torch.sigmoid(self.fc1(x))
        x = torch.sigmoid(self.fc2(x))
        return x
        
loss = torch.nn.BCELoss()
model = LogisticRegression()
optim = torch.optim.SGD(model.parameters(), lr=0.002)
zero = torch.full((100,1), 0.) # 0 for red
one = torch.full((100,1), 1.)  # 1 for blue

red_with_label  = torch.cat((red, zero), 1)
blue_with_label = torch.cat((blue, one), 1)

data = torch.cat((red_with_label, blue_with_label), 0)

accuracy = []
epochs = 100

for epoch in range(1, epochs+1):
    for x in data:
        optim.zero_grad()
        pred = model(x[:2])
        Loss = loss(pred, x[2].view(1))
        Loss.backward()
        optim.step()
        
    red_acc = model(red) < 0.5
    blue_acc = model(blue) > 0.5
    acc = torch.cat((red_acc, blue_acc), 0)

    correct = 0
    for i in acc:
        if i == True:
            correct += 1

    accuracy.append(correct / len(data))
    
    print('Epoch {:3d}/{} Cost: {:.4f}'.format(
        epoch, epochs, accuracy[-1]
    ))

plt.plot(accuracy)

---

매일 포스팅하기가 목표였는데 매주 포스팅하기로 바꿔야겠다.

다음 글에서는 오늘 살펴본 이진 분류가 아니라 Multinomial Logistic Regression(다중 회귀 분류)를 살펴보자.